返回

人工晶状体屈光力计算公式在儿童Ⅱ期植入的研究进展

阅读量：5386
DOI：10.12419/24070203
发布日期：2024-06-28
作者：
邹颖诗 ,金佳昕 ,刘臻臻 ,刘奕志
展开更多

关键词

儿童无晶状体眼
Ⅱ期人工晶状体植入
人工晶状体屈光力计算公式

摘要

Ⅱ期人工晶状体(intraocular lens,IOL)植入常用于矫正先天性白内障摘除术后无晶状体眼状态。IOL屈光力计算是影响儿童Ⅱ期IOL植入术后视功能发育和改善的关键因素之一。现有IOL屈光力计算公式是基于成人有晶状体眼的数据研发，能准确预测成人眼IOL植入的屈光力，但是对儿童Ⅱ期IOL植入的屈光力预测准确性欠佳，主要原因包括：1)儿童II期植入术前为无晶状体眼，缺乏部分公式定义中的有晶状体眼的前房深度(是指从角膜前表面中央顶点到晶状体前表面的距离)和晶状体厚度。2)公式根据囊袋内植入IOL预测屈光力，但儿童Ⅱ期IOL睫状沟植入术在临床上应用更为广泛。当IOL植入睫状沟时有效晶状体位置发生前移，可能引起屈光预测误差。3)成人眼的发育已完成，目标屈光度多为正视或近视眼(-3.00 ~ +1.00 D)，但是儿童眼仍在发育，需针对其特性测算合适的远视目标屈光度(+0.50 ~ +12.00 D)以适应眼球发育引起的屈光变化。为使Ⅱ期IOL植入患儿达到术前预设的目标屈光度，对现有公式进行选择与优化至关重要。

全文

文章亮点

1. 关键发现

  现有 IOL 屈光力计算公式在儿童Ⅱ期植入中的局限性：目前使用的 IOL 屈光力计算公式主要基于成人有晶状体眼的数据研发，对于儿童无晶状体眼的Ⅱ期 IOL 植入预测准确性较差。研究显示，这些公式在成人中的预测误差 95.6% ～ 97.8%可控制在 ±1.00 D 范围内，但在儿童中只有 16.7%-70.8% 的患者能达到这一标准。

2. 已知与发现

  现有 IOL 屈光力计算公式的分类：现有公式不断迭代更新可以分为以下 5 类：1) 根据历史经验或者术前验光值的计算方法；2) 回归公式；3) 光学透镜公式；4) 人工智能方法；5)Ray-tracing 光线追踪方法。

3. 意义与改变

  总结潜在的提高预测准确性的策略及提供未来研究方向：文章总结了几种可能的策略来提高儿童Ⅱ期植入 IOL 屈光力预测准确性，包括引入新的眼球生物参数、直接调整 IOL 屈光力、优化公式中的有效晶状体位置预测等等，强调开发专门针对儿童的新型 IOL 屈光力计算公式的必要性。
     
       Ⅱ期人工晶状体(intraocular lens, IOL)植入常用于矫正先天性白内障摘除术后无晶状体眼状态。IOL屈光力计算是影响儿童Ⅱ期IOL植入术后视功能发育和改善的关键因素之一[1-7]。
  现有IOL屈光力计算公式是基于成人有晶状体眼的数据开发，能准确预测成人眼IOL植入的屈光力，但是对儿童Ⅱ期IOL植入的屈光力预测准确性欠佳。在成人白内障研究中，可以使95.6%～97.8%患者的术后屈光预测误差控制在±1.00 D范围以内[8]。而在儿童Ⅱ期IOL植入的相关研究中，预测误差较大，仅有16.7%～70.8%患者的术后屈光预测误差控制在±1.00 D范围以内[9-10]，表现远不如成人眼。
  公式对该人群的屈光力预测准确性欠佳，主要与儿童无晶状体眼的特点有关：缺乏部分公式中有晶状体眼的前房深度(anterior chamber depth, ACD)和晶状体厚度(lens thickness, LT)，以及中高度远视目标屈光度需求。
  IOL屈光力是恒定的，但是由于小儿眼轴长度(axial length, AL)、角膜曲率(keratometry, K)等眼球生物参数仍在随着儿童年龄的增长而不断变化，从而导致屈光状态的不断变化，为患儿选择合适的术后目标屈光度增加了难度。目前研究的主流观点倾向于综合考虑患儿的各时期眼球发育的规律、近视漂移的程度、对侧眼屈光状态、是否存在弱视及弱视严重程度等多方面因素，为患儿保留一定的远视度数，然后随着年龄增长所保留的远视度数将逐渐减少。目前已有许多学者根据患儿年龄规划相应的术后目标屈光度[4, 11-15]。Baradaran-Rafii等[12]和Trivedi等[16]提出了依据儿童IOL植入手术年龄，从1月龄到14岁保留+0.50 ~ +12.00 D远视度数的具体参考方案。
  为使患儿达到术前预设的目标屈光度，对现有公式进行选择与优化至关重要。掌握基于成人有晶状体眼数据建立的公式的演变及其计算预测的关键，明确现有公式在儿童Ⅱ期IOL植入中的研究现状，以及深入了解优化公式预测准确性的方法，可以为评价儿童Ⅱ期IOL 植入的屈光力并提高预测准确性提供科学依据。

1 基于成人有晶状体眼开发的公式与有效晶状体位置的预测

  自20世纪70年代以来，先后有学者利用成人有晶状体眼的数据，研发了IOL屈光力计算公式，然后不断更新迭代[17-19]。依据Koch等[20]和Savini等[21]的研究，现有公式可以分为以下5类(图1)。

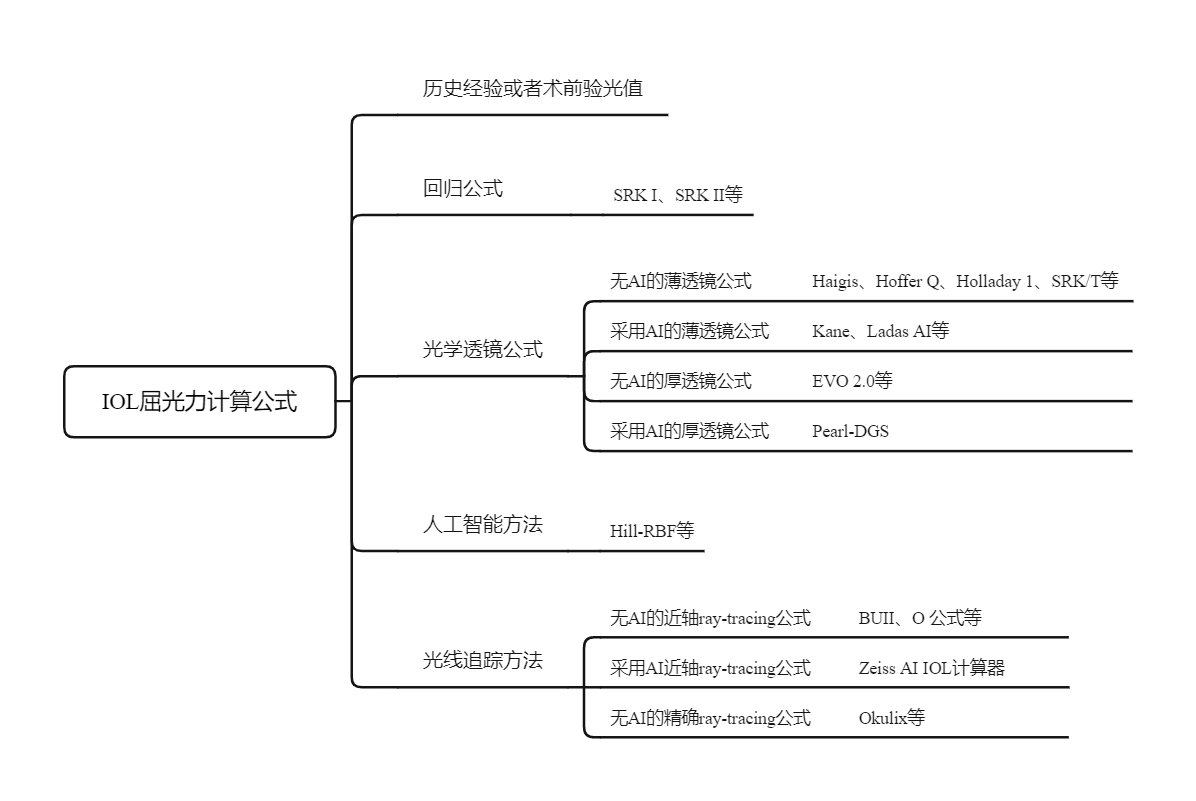
 图 1 IOL屈光力计算公式的分类
Figure 1 Classification of IOL power calculation formulas
1) 根据历史经验或者术前验光值的计算方法。
2) 回归公式，如Sanders Retzlaff-Kraff(SRK)I、SRK Ⅱ公式。
3) 光学透镜公式：需要分为薄透镜公式和厚透镜公式，以及是否采用了人工智能(artificial intelligence, AI)方法进行计算优化：①无AI的薄透镜公式，如Haigis、Hoffer Q、Holladay 1、Sanders Retzlaff-Kraff/Theoretical(SRK/T)等；②采用AI的薄透镜公式，如Kane、Ladas Artificial Intelligence Super(Ladas AI)等；③无AI的厚透镜公式，如Emmetropia Verifying Optical(EVO)2.0等；④采用AI的厚透镜公式，如Pearl-DGS。
4) AI方法，如Radial Basis Function(Hill-RBF)等。
5) Ray-tracing光线追踪方法，根据是否采用AI方法计算优化进一步划分：①无AI的近轴ray-tracing公式，如Barrett Universal II(BUII)、O公式、Olsen公式等；②采用AI近轴ray-tracing公式，如Zeiss AI IOL计算器(未公开)等；③无AI的精确ray-tracing公式，如Okulix、Olsen ray tracing(Pentacam随机公式)等。
  引入有效晶状体位置(effective lens position, ELP)概念后，IOL屈光力计算公式的预测准确性得到优化和发展。ELP指将IOL视为厚度形态忽略不计的薄透镜时其所处的屈光平面，是术前对于术后IOL囊袋内位置的预测，即角膜前表面中央顶点至IOL光学面距离。0.23 mm的ELP预测误差可以导致0.46 D的屈光预测误差[21-26]。IOL屈光力计算公式预测ELP(图2)从最开始的固定值，到引入AL和K两项眼球生物参数，如Hoffer Q、Holladay 1、SRK/T公式。Holladay 1公式的ELP由ACD和SF(晶状体常数)构成，其中ACD细分为固定的角膜厚度(0.56 mm)和根据修正Fyodorov方法计算的角膜高度[27]。SRK/T公式的ELP是基于角膜高度(也是依据修正的Fyodorov方法计算)和偏移量Offset(源自IOL常数)计算[28]。Hoffer Q公式与Holladay 1和SRK/T公式不同，它利用眼轴长度、角膜屈光力及人工晶状体常数计算ELP[29]。随着公式的发展，对ELP的估算陆续增加了ACD、LT、角膜白到白(white-to-white, WTW)等参数，如Haigis、BUⅡ公式。研究者在利用AL和K的基础上，增加术前ACD参数，能更准确地预测ELP，提高了公式的预测准确性，如Haigis公式。相比Hoffer Q、Holladay 1和SRK/T公式，Haigis公式预测误差在±0.50 D内的眼数占比提高至77%[8]；如果再增加ACD和LT等参数，如BUII公式，可以使97%患者的术后屈光预测误差控制在±1.00 D以内[30]。

图 2 ELP的预测演变
Figure 2 Prediction evolution of ELP
  因为目前大部分的IOL计算公式是基于普通成人白内障患者的数据研发，特殊白内障患者(如解剖参数异常、合并其他眼病或眼部手术史等)占比较低，这些特殊白内障患者的ELP与正常人群存在较大差异，公式的预测准确性也随之下降。如Zhang等[31]在211例(211眼)行联合硅油取出与白内障手术的患者中，发现约20%的患者屈光预测误差＞1.00 D。

2 公式对儿童Ⅱ期IOL植入的屈光力预测准确性欠佳及其原因分析

  目前，现有公式对儿童Ⅱ期IOL植入的屈光力预测准确性研究结论不一，国内外学者集中分析了回归公式(SRK Ⅱ)和传统无AI的薄透镜公式(SRK/T、Holladay 1、Hoffer Q)，缺乏相关研究评估新一代公式在儿童Ⅱ期植入的屈光力预测准确性，如BUII、EVO 2.0、Ladas AI等公式。
  公式对儿童Ⅱ期IOL植入的屈光力预测准确性远不如对成人白内障患者的屈光力预测准确性。在成人白内障研究中，可以使95.6%～97.8%患者的术后屈光预测误差控制在±1.00 D以内[8]。Chang等[9]回顾性纳入44例(65眼)接受Ⅱ期IOL植入的儿童，该研究发现相比SRK Ⅱ和Holladay 1公式，Hoffer Q和SRK/T公式在儿童Ⅱ期IOL囊袋内植入的屈光力预测准确性相对较好，分别有51.3%和53.8%患者的术后屈光预测误差控制在±1.00 D范围以内；SRK/T公式在儿童Ⅱ期IOL睫状沟植入的屈光力预测准确性优于SRK Ⅱ、Holladay 1和Hoffer Q公式，有70.8%患者的术后屈光预测误差控制在±1.00 D范围以内。Nakhli等[32]回顾性比较了75眼应用SRK II和SRK/T公式的预测准确性，发现SRK II公式比SRK/T公式预测准确性差，更易出现近视漂移(等效球镜度SRK II−4.06 D vs. SRK/T −0.21 D, P < 0.001)。Shenoy等[10]回顾性分析了104例(174眼)接受Ⅱ期IOL植入的患儿，应用SRK Ⅱ公式计算IOL屈光力的预测准确性，结果发现术后3个月平均预测误差为(1.65±2.46) D、范围为–3.25~7.50 D，绝对预测误差均值是(2.15±1.68) D、范围为 0~7.50 D，仅有20%患儿的术后屈光预测误差控制在±0.50 D以内。三项研究的结论并不一致，研究对象手术年龄的差异可能是导致不同研究结果的关键因素之一，赵云娥等的研究中，囊袋组Ⅱ期植入年龄为(35.74±16.19)月龄，睫状沟组为(28.08±6.76)月龄，Koch等的研究Ⅱ期植入年龄均小于30月龄，Shenoy等的研究Ⅱ期植入年龄为(6.08±3.75)岁。
  有学者利用术前无晶状体眼屈光力(儿童Ⅱ期IOL植入术前主觉验光的等效球镜度)来推算IOL屈光力，预测准确性仍不理想，这些研究认为当眼球生物测量困难时，可以选择性利用该方法辅助IOL屈光力[9, 32-35]。由于患儿在做检查时配合性较差，难以完成眼轴测量等必要术前检查，Hug等[33]在2004年提出了利用术前无晶状体眼屈光力来推算IOL屈光力的方法。随后，Khan和AlGaeed两位学者同样针对患儿检查欠配合的问题，提出了更复杂巧妙地利用无晶状体眼屈光力推算IOL屈光力的过程[34]。Abdel-Hafez等[35]的一项回顾性研究比较了Hug's和Khan方法以及Holladay 1公式在20眼Ⅱ期IOL植入的儿童患者中的屈光力预测准确性。研究发现Hug's 和Khan法这两者之间的预测准确性比较差异无统计学意义，Hug's 和Khan法与Holladay 1公式的预测准确性差异也不存在统计学意义。Holladay 1公式有25%的术后预测误差超过±2.00 D，但是Hug's法有40%的术后预测误差超过±2.00 D，Khan法有55%的术后预测误差超过±2.00 D。Nakhli等[32]进行了一项回顾性研究，纳入31例(31眼)接受Ⅱ期IOL植入的患儿，对比分析了眼轴聚散度公式(SRK Ⅱ、SRK/T、Holladay 1和Hoffer Q)和无晶状体眼屈光力聚散度公式(Lanchulev、Holladay-R、Mackool和Khan)的屈光力预测准确性。研究结果显示，眼轴聚散度公式的预测准确性比无晶状体眼屈光力聚散度公式更好，但眼轴聚散度公式的预测准确性仍不理想。这与Chang等[9]的研究结果一致，眼轴聚散度公式(SRK Ⅱ、SRK/T、Holladay 1和Hoffer Q)的预测准确性比无晶状体眼屈光力推算法(Hug's和Khan法)更好。因此，学者们建议开发一个专门用于儿童Ⅱ期植入的IOL屈光力计算新公式。
  现有公式是基于成人有晶状体眼的数据开发，并且是基于囊袋内植入位置来预测ELP，对儿童Ⅱ期植入IOL屈光力预测不理想的原因主要有以下三点：
1) 儿童Ⅱ期植入术前为无晶状体眼，缺乏部分公式定义中的有晶状体眼的ACD(指从角膜前表面中央顶点到晶状体前表面的距离)和LT的数值。部分IOL屈光力计算公式需要3个或者以上的眼球生物学参数预测ELP，如Haigis、Kane、Hill-RBF等公式必须有晶状体眼的ACD的数值，限制了其在儿童Ⅱ期IOL植入的使用[36-41]。
2) 公式根据IOL囊袋内植入来预测屈光力，但由于晶状体囊袋残余量不足或前后粘连严重难以重新打开，儿童Ⅱ期IOL睫状沟植入在临床上应用更广泛[2, 7, 10, 42]。在我们团队关于儿童Ⅱ期IOL植入的相关研究中，囊袋组的眼数均少于睫状沟组[1- 2]。由于IOL植入睫状沟比植入囊袋内的位置更靠前，术后患者的屈光状态会向近视漂移。在成人Ⅱ期IOL植入的研究中，发现睫状沟植入的患者在术后出现了–0.40~1.00 D的近视漂移[43-45]。
3) 成人眼的发育已完成，目标屈光度多为正视或近视眼(–3.00 ~ +1.00 D)，但是儿童眼仍在发育，眼轴长度AL、K等眼球生物参数仍在随着儿童年龄的增长而不断变化，从而导致屈光状态的不断变化，需要为患儿计算合适的远视目标屈光度(+0.50 ~ +12.00 D)，以适应术后因眼球发育导致的屈光状态改变[4, 11-13, 15]。目前已有许多学者根据患儿年龄制定了术后目标屈光状态。Baradaran-Rafii等[12]和,Trivedi等[16]提出依据儿童IOL植入手术年龄，从1月龄至14岁保留+0.50~+12.00 D远视度数的具体参考方案。Kane、Hill-RBF、Pearl-DGS等公式的目标屈光度中远视最高值小于等于+3.00 D，不能满足幼龄患儿的中高度远视目标屈光度需求。
  关于公式是否需要ACD和LT，以及目标屈光度范围总结见表1。

表 1 临床常用的IOL屈光力计算公式表
Table 1 IOL power calculation formulas in clinical practice

公式#*

是否需要ACD

是否需要

LT

目标屈光度

范围/D

SRK/T、Holladay 1、Hoffer Q

否

否

/

BUII

选择性

选择性

－10.00~+10.00 

Ladas AI Super

选择性

选择性

－10.00~+10.00

EVO 2.0

选择性

选择性

－5.00~+5.00

Haigis 

是

否

/

Kane

是

选择性

－6.00~+2.00

Pearl-DGS

是

选择性

－6.00~+3.00

Hill- RBF

是

是

－2.50~+1.00

 

3 提高IOL屈光力预测准确性的方法及其在儿童Ⅱ期IOL植入应用现状

  由于大部分IOL计算公式是基于普通白内障患者的数据研发，特殊白内障患者(如解剖参数异常、合并其他眼病或眼部手术史等)的屈光力预测准确性仍然欠佳，如本研究所涵盖的接受Ⅱ期IOL植入的儿童无晶状体眼、高度近视眼、硅油眼、短眼轴、角膜屈光术后等。提高IOL屈光力预测准确性，特别是针对这些特殊白内障患者，成为国内外学者关注的焦点。根据目前文献报道，提高这些特殊人群的IOL屈光力预测准确性的方法，包括但不限于以下6种。

3.1 引入新的眼球生物参数

  随着眼前节测量仪器的发展，可以更精准地测量和挖掘更多的眼球生物参数指标，公式可以利用越来越多的眼球生物参数来预测ELP，不断提高屈光力预测准确性。
  现有公式中利用的是模拟角膜曲率(simulated K, simK)，即根据前表面K和Gullstrand模型眼推测出来的曲率。随着设备的更新，目前可以获得全角膜曲率(total K,TK)。不少研究比较了TK和sim K对公式预测准确性的影响。Wei等[46]在超高度近视眼并发性白内障的人群中发现，在角膜较薄的超高度近视眼中，与传统的K相比，TK具有更小的绝对预测误差。Qin等[47]发现当角膜比较平坦(K≤42 D)或者陡峭(K≥46 D)时，公式使用TK值可获得更好的预测准确性。
  除了LT，晶状体其他参数也会对ELP产生影响，如晶状体拱高(lens vault, LV)。Yan等[48]发现了LV对浅前房患者(ACD＜3 mm)的IOL屈光力预测准确性产生影响。当浅前房患者的LV≥0.95 mm时，应用Haigis和Hoffer QST公式会产生较大的预测误差。
  儿童Ⅱ期植入前为无晶状体眼，可以利用眼前节测量仪器获得无晶状体眼的ACD数值[32, 49-52]。无晶状体眼ACD对公式预测准确性的影响，以及在公式中引入无晶状体眼的ACD能否进一步提高预测准确性，目前尚未见报道。

3.2 直接调整IOL屈光力

  直接调整IOL屈光力的方法可用于调整睫状沟植入的IOL屈光力。公式计算的是囊袋内植入IOL屈光力，当由于外伤等原因导致囊膜缺如或支撑不足，需要将IOL放置于睫状沟，会导致ELP发生前移，引起屈光预测误差。既往研究建议术者下调IOL屈光力(按植入囊袋内计算)后再植入睫状沟，从而降低近视误差。Dubey等[43]认为，在SRK/T公式计算的基础上，IOL预测屈光力＜18 D时，应降低0.5 D；IOL预测屈光力在18~25 D内，应至少降低1 D；IOL预测屈光力＞25 D，应降低1.5~2.0 D。也有学者建议睫状沟植入屈光力应比预测屈光力减少5%屈光力[44]。经典的IOL屈光力调整方案是依据SRK/T公式推算得到的；由于不同公式对ELP的预测存在差异，经典的调整方案在新公式中的表现尚需进一步验证。此外，睫状沟的位置与患者眼球的生物学参数密切相关，根据眼球解剖结构与IOL类型个性化调整ELP预测能进一步提高预测准确性。
  现有关于睫状沟植入屈光力调整的研究人群多为成人无晶状体眼，缺乏儿童Ⅱ期IOL植入的相关研究，尚无统一公认的儿童Ⅱ期IOL睫状沟植入屈光力的调整方案。

3.3 优化公式中的ELP预测

  ELP预测受到眼部解剖结构差异、IOL材料及设计差异、眼科手术操作等因素的影响[26]。部分特殊白内障患者的眼部解剖参数存在异常，如原发性闭角型青光眼患者眼前段狭小和结构拥挤：前房浅、眼轴短、房角窄、角膜小、晶状体大等[53]；如晶状体脱位患者前房深浅不一，影响ACD和LT测量[22]。当患者的眼球解剖参数偏离人群平均值时，ELP与正常人群存在较大差异，公式的预测准确性下降。
  为了提高这些特殊人群的屈光力预测准确性，学者们开展了优化公式中ELP预测的研究，通过线性回归分析建立ELP优化预测方程，再代入原公式中推导，此类方法适用于可获取完整计算步骤的公式，如Hoffer Q、Holladay 1、SRK/T和Haigis等公式。Ding等[53]针对原发性闭角型青光眼患者，通过引入虹膜根部深度(iris root depth, IRD)参数来优化ELP的预测，先利用UBM测量获得IRD数值，然后通过线性逐步回归分析，建立由IRD、AL、LT组成的ELP预测方程，并代入 Haigis公式，获得HaigisIRD公式。研究发现HaigisIRD公式的准确性显著高于原Haigis公式，与Kane公式准确性相似。Zou等[22]针对晶状体脱位患者，通过引入一个新的中间变量Z参数来优化ELP的预测，定义为虹膜平面至IOL平面的距离，在SRK/T公式中代入优化后的ELP进行IOL屈光力的计算。研究发现能够提高晶状体脱位患者的屈光力预测准确性，64%患者的预测误差可以控制在±0.25 D以内。
  公式是根据囊袋内植入IOL来预测屈光力，当IOL植入位置发生改变，如睫状沟植入会导致ELP发生前移，从而产生预测误差。Eom等[54]针对睫状沟植入的成人眼，利用线性回归分析，基于Haigis公式改良ELP预测方程，研发了EOM'S 睫状沟植入屈光力计算器。与单纯调整睫状沟IOL植入屈光力相比，优化Haigis公式的ELP预测，可以使预测误差控制在±1.00 D以内的眼数百分比从78.3%提高到98.6%。
  儿童Ⅱ期IOL睫状沟植入在临床上更为广泛，利用线性回归分析，基于可获取完整计算步骤的公式，优化儿童Ⅱ期IOL睫状沟植入的ELP预测，是否可以提高屈光力预测准确性，有待进一步研究。

3.4 眼球生物参数调整法

   眼球生物参数调整法多用于眼球解剖异常或者因眼部条件影响眼球生物测量准确性的特殊白内障患者，如高度近视并发性白内障患者可能存在后巩膜葡萄肿，影响眼轴测量，学者们提出了Wang-Koch眼轴调整法、Cooke-modified法[55-56]；又如角膜屈光术后患者，发生了K、AL的改变，学者们提出了角膜屈光术后中央角膜屈光力的Shammas法等[57]。Zhang等[56]回顾性纳入164眼超高度近视眼并发性白内障患者(眼轴≥26 mm)，研究发现Holladay 1和SRK/T公式结合Wang-Koch眼轴调整法的预测准确性，与BUII、EVO、Ladas AI准确性相似。
  接受Ⅱ期IOL植入的儿童眼，因检查欠配合，眼球生物测量数值仅供参考，或者存在偏离成人眼的眼球生物参数数值等情况，是否可以通过调整眼球生物参数提高预测准确性，有待深入研究。

3.5 IOL常数优化法

  IOL常数是IOL屈光力计算公式的重要参数之一。IOL常数优化是通过调整常数，移动IOL屈光力公式的预测曲线，从而消除系统误差的方法，能有效提高IOL计算公式的预测准确性[58]。Aristodemou等[58]发现经过IOL常数优化，可以使得预测误差在0.50 D以内的眼数占比从42%提高到71%。IOL常数优化的方法可以分成4类：ELP法、ULIB数据库、仪器内置程序、临床矫正法。IOL常数优化建议先进行样本的生物测量的统计分析，排除异常值，至少纳入148~257眼。IOL常数优化存在以下问题：第一，未能解决误差分布的离散问题，这与公式的选择关系更大；第二，如果样本不符合正态分布，优化结果会受到生物测量数据权重较大的影响，造成偏移，第三，需要对每一种类型的IOL收集大量数据，一些罕见眼病的特殊人群不一定有充足的样本量[59-61]。关于接受Ⅱ期IOL植入的儿童眼是否适合进行IOL常数优化，尚需进一步研究明确。

3.6 开发新公式

  近年来不断有学者针对特殊人群的眼球生物参数特点研发了新公式。郭海科等[62]针对角膜屈光手术后人群，研发了在线的计算器，绝对预测误差均值为0.62 D，且83.7%的预测误差控制在±0.50 D以内。Guo等[63]专门针对高度近视眼研发了Zhu-Lu公式。Zhu-Lu公式在高度近视眼人群中具有良好的屈光力预测准确性，在超高度近视眼中表现也良好。与其他公式(BUII、EVO 2.0、Kane、Pearl-DGS和RBF公式)相比，Zhu-Lu公式预测误差在±0.50 D以内的眼数占比最高，其中内部数据集80.61%、外部数据集72.85%，其他公式的眼数占比在内部数据集为53.19%～72.85%、外部数据集为63.58%～70.86%。Zhang等[64]针对玻璃体切割术后白内障患者研发了Lisa-PPV公式。与其他公式(BUII、EVO 2.0、Hoffer-QST、Kane、Ladas AI、Pearl-DGS和RBF公式)相比，Lisa-PPV公式预测误差在±0.50 D范围以内的眼数占比最高，为57.14%，其他公式是37.50%～40.63%。由于接受Ⅱ期IOL植入的儿童眼对公式选择的特殊性：缺乏部分公式定义中的晶状体眼的ACD和LT，以及远视目标屈光度需求，应针对该人群特点研发新公式。

利益冲突

所有作者均声明不存在利益冲突。

开放获取声明

本文适用于知识共享许可协议(Creative Commons)，允许第三方用户按照署名(BY)-非商业性使用(NC)-禁止演绎(ND)(CC BY-NC-ND)的方式共享，即允许第三方对本刊发表的文章进行复制、发行、展览、表演、放映、广播或通过信息网络向公众传播，但在这些过程中必须保留作者署名、仅限于非商业性目的、不得进行演绎创作。详情请访问：https://creativecommons.org/licenses/by-nc-nd/4.0/。

基金

1、广东省自然科学基金(2023A1515011102)。
This work was supported by the Natural Science Foundation of Guangdong Province of China ( 2023A1515011102).

参考文献

1、Liu Z, Zou Y, Yu Y, et al. Accuracy of intraocular lens power calculation in pediatric secondary implantation: In-the-bag versus sulcus placement[ J]. Am J Ophthalmol, 2023, 249: 137-143. DOI: 10.1016/ j.ajo.2022.12.028.
2、Liu Z, Lin H, Jin G, et al. In-the-bag versus ciliary sulcus secondary intraocular lens implantation for pediatric aphakia: a prospective comparative study[ J]. Am J Ophthalmol, 2022, 236: 183-192. DOI: 10.1016/j.ajo.2021.10.006.
3、刘奕志, 吴明星. 先天性白内障的手术治疗及展望[J]. 中 国眼耳鼻喉科杂志, 2017, 17(2): 79-81+84. DOI: 10.14166/ j.issn.1671-2420.2017.02.001.
Liu YZ, Wu MX. Advances and outlook of congenital cataract surgery[J]. Chin J Ophthalmol Otorhinolaryngol, 2017, 17(2): 79- 81+84. DOI: 10.14166/j.issn.1671-2420.2017.02.001.
4、陈伟蓉. 先天性白内障手术治疗的思考 [ J]. 中华眼科杂志, 2021, 57(1): 11-6. Doi: 10.3760/cma.j.cn112142-20201022-00697.
Chen WR. Reflections on surgical treatment of congenital cataract [ J]. Chin J Ophthalmol, 2021, 57(1): 11-6. Doi: 10.3760/cma.j.cn112142- 20201022-00697.
5、Lalwani S, Kekunnaya R. Secondary intraocular lens implantation (IOL) in children- what, why, when, and how?[ J]. Semin Ophthalmol, 2023, 38(3): 255-264. DOI: 10.1080/08820538.2022.2116288.
6、VanderVeen DK , Drews-Botsch CD, Nizam A, et al. Outcomes of secondary intraocular lens implantation in the Infant Aphakia Treatment Study[ J]. J Cataract Refract Surg, 2021, 47(2): 172-177. DOI: 10.1097/j.jcrs.0000000000000412.
7、Koch CR, Kara-Junior N, Serra A, et al. Long-term results of secondary intraocular lens implantation in children under 30 months of age[ J]. Eye, 2018, 32(12): 1858-1863. DOI: 10.1038/s41433-018-0191-3.
8、Melles RB, Holladay JT, Chang WJ. Accuracy of intraocular lens calculation formulas[ J]. Ophthalmology, 2018, 125(2): 169-178. DOI: 10.1016/j.ophtha.2017.08.027.
9、Chang P, Li Z, Zhang F, et al. Comparison of aphakic refraction and biometry-based formulae for secondary In-the-bag and sulcus-implanted intraocular lens power estimation in children[ J]. Ophthalmic Res, 2021, 64(6): 1048-1054. DOI: 10.1159/000512753.
10、Shenoy BH, Mittal V, Gupta A, et al. Refractive outcomes and prediction error following secondary intraocular lens implantation in children: a decade-long analysis[ J]. Br J Ophthalmol, 2013, 97(12): 1516-1519. DOI: 10.1136/bjophthalmol-2012-302775.
11、陈伟蓉, 陈卉, 林浩添. 先天性白内障治疗现状及展望[ J]. 中华 眼视光学与视觉科学杂志, 2018, 20(1): 1-6+13. DOI: 10.3760/ cma.j.issn.1674-845X.2018.01.001.
Chen WR, Chen H, Lin HT. Status and prospect of congenital cataract treatment[ J]. Chin J Optom Ophthalmol Vis Sci, 2018, 20(1): 1-6+13. DOI: 10.3760/cma.j.issn.1674-845X.2018.01.001.
12、Baradaran-Rafii A, Shirzadeh E, Eslani M, et al. Optical correction of aphakia in children[ J]. J Ophthalmic Vis Res, 2014, 9(1): 71-82.
13、Al Shamrani M, Al Turkmani S. Update of intraocular lens implantation in children[ J]. Saudi J Ophthalmol, 2012, 26(3): 271-275. DOI: 10.1016/j.sjopt.2012.05.005.
14、冯张青, 李俊红. 重视儿童白内障手术时机、手术方法及术后 并发症处理方式的选择[ J]. 中华眼科医学杂志(电子版), 2019, 9(1): 1-6. DOI: 10.3877/cma.j.issn.2095-2007.2019.01.001. Feng ZQ, Li JH. Pay attention to the choice of operation time, operation method and treatment of complications after cataract surgery in children[ J]. Chin J Ophthalmol Med (Electron Ed), 2019, 9(1): 1-6. DOI: 10.3877/cma.j.issn.2095-2007.2019.01.001.
15、Sachdeva V, Katukuri S, Kekunnaya R, et al. Validation of guidelines for undercorrection of intraocular lens power in children[ J]. Am J Ophthalmol, 2017, 174: 17-22. DOI: 10.1016/j.ajo.2016.10.017.
16、Trivedi RH, Wilson ME. Pediatric cataract: preoperative issues and considerations[M]//Wilson M, Trivedi R , Saunders R . Pediatric Ophthalmology. Berlin, Heidelberg: Springer, 2009: 311- 324.10.1007/978-3-540-68632-3_22.
17、张玉婷, 赵春梅, 刘湘云, 等. 人工晶状体度数计算公式的研 究现状[ J]. 国际眼科杂志, 2021, 21(3): 462-466. DOI: 10.3980/ j.issn.1672-5123.2021.3.17.
Zhang YT, Zhao CM, Liu XY, et al. Research status of the formulas for calculating the degree of intraocular lens[ J]. Int Eye Sci, 2021, 21(3): 462-466. DOI: 10.3980/j.issn.1672-5123.2021.3.17.
18、向菁, 管怀进. 人工晶状体计算公式的研究进展[ J]. 眼科新进 展, 2018, 38(6): 583-587. DOI: 10.13389/j.cnki.rao.2018.0138.
Xiang J, Guan HJ. Research progress on the calculation formulas of IOL[ J]. Recent Adv Ophthalmol, 2018, 38(6): 583-587. DOI: 10.13389/j.cnki.rao.2018.0138.
19、李鑫鑫, 李绍伟. 新型人工晶状体屈光度数计算公式的研究进 展[ J]. 中华眼科杂志, 2022, 58(7): 544-548. DOI: 10.3760/cma. j.cn112142-20211003-00468.
Li XX, Li SW. Research progress of new generation intraocular lens calculation formulas[ J]. Chin J Ophthalmol, 2022, 58(7): 544-548. DOI: 10.3760/cma.j.cn112142-20211003-00468.
20、Koch DD, Hill W, Abulafia A, et al. Pursuing perfection in intraocular lens calculations: I. Logical approach for classifying IOL calculation formulas[J]. J Cataract Refract Surg, 2017, 43(6): 717-718. DOI: 10.1016/j.jcrs.2017.06.006.
21、Savini G, Hoffer KJ, Kohnen T. IOL power formula classifications[ J]. J Cataract Refract Surg, 2024, 50(2): 105-107. DOI: 10.1097/ j.jcrs.0000000000001378.
22、Zou M, Lian Z, Young CA, et al. Improving effective lens position prediction for transscleral fixation of intraocular lens among congenital ectopia lentis patients[ J]. Am J Ophthalmol, 2023, 252: 121-129. DOI: 10.1016/j.ajo.2023.03.021.
23、Kane JX, Chang DF. Intraocular lens power formulas, biometry, and intraoperative aberrometry: a review[ J]. Ophthalmology, 2021, 128(11): e94-e114. DOI: 10.1016/j.ophtha.2020.08.010.
24、Stopyra W, Langenbucher A, Grzybowski A. Intraocular lens power calculation formulas-a systematic review[ J]. Ophthalmol Ther, 2023, 12(6): 2881-2902. DOI: 10.1007/s40123-023-00799-6.
25、Kothari SS, Reddy JC. Recent developments in the intraocular lens formulae: an update[ J]. Semin Ophthalmol, 2023, 38(2): 143-150. DOI: 10.1080/08820538.2022.2094712.
26、李修远, 常平骏, 赵云娥. 人工晶状体屈光度计算公式中有效晶 状体位置的预测及其影响因素[ J]. 国际眼科纵览, 2021, 45(5): 409-414. DOI: 10.3760/cma.j.issn.1673-5803.2021.05.008.
Li XY, Chang PJ, Zhao YE. Prediction of effective lens position in intraocular lens calculation formula and its influencing factors[ J]. Int Rev Ophthalmol, 2021, 45(5): 409-414. DOI: 10.3760/cma. j.issn.1673-5803.2021.05.008.
27、Holladay JT. Standardizing constants for ultrasonic biometry, keratometry, and intraocular lens power calculations[J]. J Cataract Refract Surg, 1997, 23(9): 1356-1370. DOI: 10.1016/s0886- 3350(97)80115-0.
28、Retzlaff JA, Sanders DR , Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula[ J]. J Cataract Refract Surg, 1990, 16(3): 333-340. DOI: 10.1016/s0886- 3350(13)80705-5.
29、Hoffer KJ. The Hoffer Q formula: a comparison of theoretic and regression formulas[ J]. J Cataract Refract Surg, 1993, 19(6): 700-712. DOI: 10.1016/s0886-3350(13)80338-0.
30、Roberts TV, Hodge C, Sutton G, et al. Comparison of Hill-radial basis function, Barrett Universal and current third generation formulas for the calculation of intraocular lens power during cataract surgery[ J]. Clin Exp Ophthalmol, 2018, 46(3): 240-246. DOI: 10.1111/ ceo.13034.
31、Zhang J, Han X, Chen X, et al. Choice of intraocular lens calculation formula for cataract patients with prior pars Plana vitrectomy[ J]. J Cataract Refract Surg, 2023, 49(9): 956-963. DOI: 10.1097/j.jcrs.0000000000001253.
32、Nakhli FR, Emarah K, Jeddawi L. Accuracy of formulae for secondary intraocular lens power calculations in pediatric aphakia[ J]. J Curr Ophthalmol, 2017, 29(3): 199-203. DOI: 10.1016/j.joco.2017.05.007.
33、Hug T. Use of the aphakic refraction in intraocular lens (IOL) power calculations for secondary IOLs in pediatric patients[ J]. J Pediatr Ophthalmol Strabismus, 2004, 41(4): 209-211. DOI: 10.3928/0191-3913-20040701-07.
34、Khan AO, AlGaeed A. Paediatric secondary intraocular lens estimation from the aphakic refraction alone: comparison with a standard biometric technique[ J]. Br J Ophthalmol, 2006, 90(12): 1458-1460. DOI: 10.1136/bjo.2006.100834.
35、Abdel-Hafez G, Trivedi RH, Wilson ME, et al. Comparison of aphakic refraction formulas for secondary in-the-bag intraocular lens power estimation in children[ J]. J AAPOS, 2011, 15(5): 432-434. DOI: 10.1016/j.jaapos.2011.05.021.
36、Barrett GD. An improved universal theoretical formula for intraocular lens power prediction[ J]. J Cataract Refract Surg, 1993, 19(6): 713-720. DOI: 10.1016/s0886-3350(13)80339-2.
37、Shammas HJ, Taroni L, Pellegrini M, et al. Accuracy of newer intraocular lens power formulas in short and long eyes using sum-of-segments biometry[ J]. J Cataract Refract Surg, 2022, 48(10): 1113-1120. DOI: 10.1097/j.jcrs.0000000000000958.
38、Haigis W, Lege B, Miller N, et al. Comparison of immersion ultrasound biometry and partial coherence interferometry for intraocular lens calculation according to Haigis[ J]. Graefe’s Arch Clin Exp Ophthalmol, 2000, 238(9): 765-773. DOI: 10.1007/s004170000188.
39、Kane JX, Van Heerden A, Atik A, et al. Intraocular lens power formula accuracy: comparison of 7 formulas[ J]. J Cataract Refract Surg, 2016, 42(10): 1490-1500. DOI: 10.1016/j.jcrs.2016.07.021.
40、Ladas JG, Siddiqui AA, Devgan U, et al. A 3-D “super surface”combining modern intraocular lens formulas to generate a “super formula” and maximize accuracy[ J]. JAMA Ophthalmol, 2015, 133(12): 1431-1436. DOI: 10.1001/jamaophthalmol.2015.3832.
41、Debellemanière G, Dubois M, Gauvin M, et al. The PEARL-DGS formula: the development of an open-source machine learning-based thick IOL calculation formula[ J]. Am J Ophthalmol, 2021, 232: 58-69. DOI: 10.1016/j.ajo.2021.05.004.
42、Shenoy BH, Mittal V, Gupta A, et al. Complications and visual outcomes after secondary intraocular lens implantation in children[ J]. Am J Ophthalmol, 2015, 159(4): 720-726. DOI: 10.1016/j.ajo.2015.01.002.
43、Dubey R, Birchall W, Grigg J. Improved refractive outcome for ciliary sulcus-implanted intraocular lenses[ J]. Ophthalmology, 2012, 119(2): 261-265. DOI: 10.1016/j.ophtha.2011.07.050.
44、Knox Cartwright NE, Aristodemou P, Sparrow JM, et al. Adjustment of intraocular lens power for sulcus implantation[ J]. J Cataract Refract Surg, 2011, 37(4): 798-799;authorreply 799-800. DOI: 10.1016/j.jcrs.2011.02.020.
45、Mehta R, Aref AA. Intraocular lens implantation in the ciliary sulcus: challenges and risks[ J]. Clin Ophthalmol, 2019, 13: 2317-2323. DOI: 10.2147/OPTH.S205148.
46、Wei L, Cheng K, He W, et al. Application of total keratometry in ten intraocular lens power calculation formulas in highly myopic eyes[ J]. Eye Vis, 2022, 9(1): 21. DOI: 10.1186/s40662-022-00293-3.
47、Qin Y, Liu L, Mao Y, et al. Accuracy of intraocular lens power calculation based on total keratometry in patients with flat and steep corneas[ J]. Am J Ophthalmol, 2023, 247: 103-110. DOI: 10.1016/j.ajo.2022.11.011.
48、Yan C, Yao K. Effect of lens vault on the accuracy of intraocular lens calculation formulas in shallow anterior chamber eyes[ J]. Am J Ophthalmol, 2022, 233: 57-67. DOI: 10.1016/j.ajo.2021.07.011.
49、Dooley I, Charalampidou S, Malik A, et al. Changes in intraocular pressure and anterior segment morphometry after uneventful phacoemulsification cataract surgery[ J]. Eye, 2010, 24(4): 519-526;quiz527. DOI: 10.1038/eye.2009.339.
50、Elfiky M, Saad H, Elseht R, et al. Role of ultrasound biomicroscopy in the planning for secondary implantation of intra ocular lens in aphakia[ J]. Int Ophthalmol, 2016, 36(3): 391-400. DOI: 10.1007/s10792-015-0141-z.
51、Landegger GP, Roth N. Anterior chamber depth and its stability in aphakia[ J]. Am J Ophthalmol, 1968, 65(5): 706-708. DOI: 10.1016/0002-9394(68)94385-7.
52、Norn MS. Depth of anterior chamber after cataract extraction[ J]. Br J Ophthalmol, 1978, 62(7): 474-477. DOI: 10.1136/bjo.62.7.474.
53、Ding Y, Hou M, Liu L, et al. Prediction of postoperative effective lens position using iris root depth in primary angle-closure diseases[ J]. J Cataract Refract Surg, 2023, 49(7): 691-696. DOI: 10.1097/j.jcrs.0000000000001174.
54、Eom Y, Song JS, Kim HM. Modified haigis formula effective lens position equation for ciliary sulcus-implanted intraocular lenses[ J]. Am J Ophthalmol, 2016, 161: 142-149.e1-2. DOI: 10.1016/j.ajo.2015.09.040.
55、Wang L, Shirayama M, Ma XJ, et al. Optimizing intraocular lens power calculations in eyes with axial lengths above 25.0 mm[ J]. J Cataract Refract Surg, 2011, 37(11): 2018-2027. DOI: 10.1016/j.jcrs.2011.05.042.
56、Zhang J, Tan X, Wang W, et al. Effect of axial length adjustment methods on intraocular lens power calculation in highly myopic eyes[ J]. Am J Ophthalmol, 2020, 214: 110-118. DOI: 10.1016/j.ajo.2020.02.023.
57、Wang L, Koch DD. Intraocular lens power calculations in eyes with previous corneal refractive surgery: challenges, approaches, and outcomes[ J]. Taiwan J Ophthalmol, 2021, 12(1): 22-31. DOI: 10.4103/tjo.tjo_38_21.
58、Aristodemou P, Knox Cartwright NE, Sparrow JM, et al. Intraocular lens for mula constant opt imizat ion and par t ial coherence interferometry biometry: Refractive outcomes in 8108 eyes after cataract surgery[ J]. J Cataract Refract Surg, 2011, 37(1): 50-62. DOI: 10.1016/j.jcrs.2010.07.037.
59、Langenbucher A, Hoffmann P, Cayless A, et al. Limitations of constant optimization with disclosed intraocular lens power formulae[ J]. J Cataract Refract Surg, 2024, 50(3): 201-208. DOI: 10.1097/j.jcrs.0000000000001337.
60、Langenbucher A , Szentmáry N, Cayless A , et al. IOL formula constants: strategies for optimization and defining standards for presenting data[ J]. Ophthalmic Res, 2021, 64(6): 1055-1067. DOI: 10.1159/000514916.
61、Gatinel D, Debellemanière G, Saad A, et al. A simplified method to minimize systematic bias of single-optimized intraocular lens power calculation formulas[ J]. Am J Ophthalmol, 2023, 253: 65-73. DOI: 10.1016/j.ajo.2023.05.005.
62、郭海科, 金海鹰, GerdUAUFFARTH, 等. 应用优化计算方法与计算机软件计算角膜屈光手术后人工晶状体屈光力[ J]. 中华眼视光学与视觉科学杂志, 2010, 12(6): 429-432. DOI: 10.3760/cma.j.issn.1674-845X.2010.06.007.
Guo HK, Jin HY, Gerd U, et al. Intraocular lens power calculation after corneal refractive surgery using serf-designed computer software programmed with optimized calculation method[ J]. Chin J Optom Ophthalmol Vis Sci, 2010, 12(6): 429-432. DOI: 10.3760/cma. j.issn.1674-845X.2010.06.007.
63、Guo D, He W, Wei L, et al. The Zhu-Lu formula: a machine learning-based intraocular lens power calculation formula for highly myopic eyes[ J]. Eye Vis, 2023, 10(1): 26. DOI: 10.1186/s40662-023-00342-5.
64、Zhang J, Jin A, Han X, et al. The LISA-PPV formula: an ensemble artificial intelligence-based thick intraocular lens calculation formula for vitrectomized eyes[ J]. Am J Ophthalmol, 2024, 262: 237-245. DOI: 10.1016/j.ajo.2024.02.037.

相关文章

张佳晴;谈旭华;罗莉霞,人工晶状体屈光力计算：求于至精，臻于至善陈海婷;牛广增;冯雪艳;刘逾;范玉香,中央孔后房型人工晶体植入术矫正屈光不正的疗效周开晶;梅健琪;郑琳;胡江健;俞阿勇,六种新一代人工晶状体屈光力计算公式的预测准确性比较