文章亮点

1 关键发现

• 数字化新技术 Eye-ruler2 与传统五合一测量尺相比，在瞳距、左右眼镜眼距、前倾角测量上一致性好，仅面弯一致性较差；而面弯一致性差可能源于方法学差异（传统五合一测量尺测量 vs Eye-ruler2 真实戴镜测量）及镜框材质、鼻托压力对戴镜状态面弯的动态影响。

2 已知与发现

• 既往研究仅关注镜眼距对处方的理论影响，现研究发现镜眼距与前倾角对处方等效屈光度贡献等同；且高度近视（<-6.00D）人群中，镜眼距对处方度数影响大于前倾角，与既往理论研究结果一致。

• 前倾角、面弯仅在少量个性化渐进镜验配中作为常规参数；现研究发现，中低度近视（在-6.00D以内）人群中，前倾角对处方度数影响大于镜眼距；而真实佩戴前倾角均值（5.36°）低于理论参考范围，推测可能与亚洲人鼻梁较深肤色人种更低平相关。

3 意义与改变

• 明确 Eye-ruler2 在瞳距、镜眼距、前倾角测量上的优势（操作简便、减少人为误差、受检者体验好），且可替代传统方法，为其临床推广提供直接证据，有望改变传统依赖操作者经验的测量模式，降低测量技术门槛。

• 量化镜眼距、前倾角、面弯参数对处方的影响，为 “从光学矫正到视觉质量提升” 提供数据支撑，契合当前个性化配镜、镜架定制普及的行业趋势，推动行业从 “基础光学矫正” 向 “高质量视觉服务” 转型。

       近年来，随着“十四五”全国眼健康规划工作的不断推进，人民群众的眼健康需求也在不断增长，对于视觉质量的要求也在不断提升，所以在验配过程中对于配镜参数的精准度要求也越来越高。配镜参数的精准测量是保障光学矫正效果和提升视觉质量的核心环节^[1-3]。随着测量技术的不断发展，配镜参数测量的方法也从传统手工测量（如五合一测量尺等）逐步发展为数字化技术（如Nidek PM-700、Zeiss Visufit和Essilor Eye-ruler2等），而数字化技术无论是精准度还是便捷性都有显著提升。但目前市面上可测量配镜参数的方法众多，存在测量原理、采集范围和精度不同的问题。以往对于单一瞳距参数测量差异性研究较多^[4-5]，但在临床上缺少数字化技术与手工方法测量配镜参数（如镜眼距、前倾角及面弯）之间的一致性研究。由于临床缺乏各方公认的配镜参数测量设备，因此视光师需要参考多种测量工具的结果，以提高其数据准确度。

       目前临床上常规的配镜处方主要有屈光度及瞳距两个主要参数，而镜眼距、前倾角和面弯等并不作为常规测量及计算因素。镜眼距是指角膜前顶点至镜片后表面光学中心的轴向距离^[6]，其变化可导致等效球镜度偏差（如-14.00 D的镜片, 镜眼距从12 mm变为14 mm，则计算得到有效屈光度数值变为-13.62 D）；前倾角是镜片与面部冠状面夹角^[6]，其变化可能会产生初阶像差^[7]中的水平顺规散光^[8]，影响视觉质量^[9]（如：当镜片度数为-10 D，前倾角有10度的倾斜时，实际配镜处方效果则会变为:-10.10 DS/-0.31 DC x 180）；面弯为镜框水平面的弯曲弧度^[6]，因过大或不对称而产生倾斜，可能引入非对称的垂直逆规散光^[3]；瞳距是指两眼瞳孔中心间的距离^[6]，其测量误差会导致眼镜产生棱镜效果^[3]，造成视觉不适^[10]和视疲劳^{[11, 12]}等不良影响。在临床使用试镜架或者综合验光仪验光时，镜眼距通常被认为是12 mm，前倾角和面弯度数为0，而在真实世界配镜参数则会受品牌定制、顾客的个人戴镜习惯和脸型等影响。以往有研究发现顾客戴镜不适可能与瞳距、前倾角和镜眼距等参数误差有关^[13]，但在阐述镜眼距、面弯、前倾角等参数对于实际屈光度数的影响时，仅只局限于理论推导^{[2-3, 14-15]}。

       本研究旨在评估数字化新技术（Eye-ruler2）与手动传统测量方法（五合一测量尺）在配镜参数的一致性，并进一步探索两种测量技术下相关参数对矫正处方的影响，为眼镜精准验配及视觉质量提升提供依据和思路。

1 对象和方法

1.1 研究对象

        这项研究于2024 年 12 月在广州新华学院招募了年龄在18~23岁、单眼或双眼近视且佩戴框架眼镜的在校大学生103人。所有研究对象为单纯近视或复合近视散光，排除合并其他眼部疾病、全身疾病、曾进行眼部手术和外伤史者。

       该研究已获得中山大学机构审查委员会和中山眼科中心伦理委员会的批准（批件号：2024KYPJ153）。所有程序均遵循《赫尔辛基宣言》的原则。所有参与者均已签署知情同意书。

1.2 研究流程

    1.2.1 研究流程概述

       现场收集研究对象的名字和年龄等基本数据，研究者先测量框架眼镜度数，然后使用Eye-ruler2为研究对象测量镜眼距、前倾角、面弯和瞳距参数，最后使用五合一测量尺，为同一研究对象再次测量镜眼距、前倾角、面弯和瞳距参数。总检查时间在10～15 min，上述所有测量均由同一经验丰富人员完成。

    1.2.2 配镜参数测量

    1.2.2.1 屈光度测量

        使用电脑焦度计（Nidek，LM-7P / 7）测量镜片球镜度数（DS）、柱镜度数（DC）及柱镜轴位（A），并记录左右镜片屈光度数据。

    1.2.2.2 Eye-ruler2

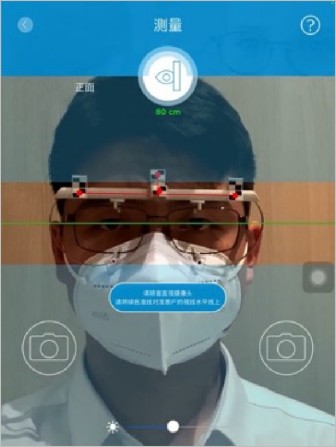
        Eye-ruler2是一款个性化配镜参数测量仪器（是基于iPad高清摄像头与图像识别算法快速获得眼镜参数的新技术），把专用的镜头放在iPad上，通过拍摄两张照片（正面和侧面）自动定位瞳孔中心和镜框几何特征，即可以获得全部的配镜参数（图1、2）。

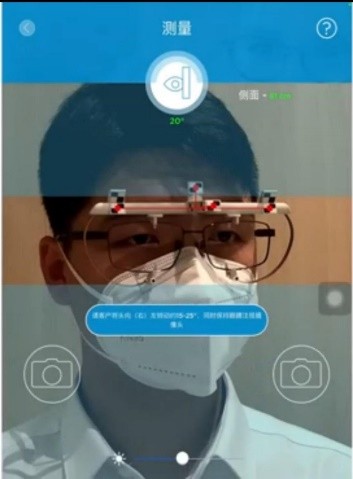
       操作步骤如下：启动Eye-ruler2并连接iPad，建立档案。将镜架居中固定于测量夹，研究对象坐姿端正，双眼平视，头部距iPad屏幕60～75 cm，且居中绿色准线。正面拍摄时（图1）需垂直放置iPad，注视摄像头拍摄，获取瞳距、镜眼距及面弯；侧面拍摄时（图2），需研究对象头部转动20°±5°，校正红色标识后拍摄，同步分析前倾角。随后进行镜框标定：用方框标记法对齐镜框内边缘，选择材质（金属/板材/无框/半框），验证并修正标记。最终系统自动输出参数（如异常，则数据标红，需重新测量）；确认后导出数据，保存原始图像及数值。

    1.2.2.3 五合一测量尺

       该工具可单独测量镜眼距、前倾角、面弯和瞳距等配镜参数。其中镜眼距和前倾角参数需在研究对象戴镜状态下测量，面弯和瞳距则在研究对象非佩戴状态下测量。

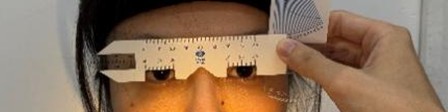
       操作步骤如下：首先进行镜眼距测量，在研究对象佩戴眼镜状态下，使用五合一测量尺测量镜片后顶点至角膜顶点的轴向距离，左右眼各测量3次计算平均值（保留小数点后一位）（图3）；然后进行前倾角测量，在研究对象自然佩戴眼镜后，测量镜片平面与面部冠状面的夹角，分别测量3次后计算平均值（保留小数点后一位）（图4）；随后进行面弯测量，使用五合一测量尺对镜架水平面弧度进行非佩戴状态下的静态测量，重复3次计算平均值（保留小数点后一位）（图5）；最后进行瞳距测量时，通过五合一测量尺测量研究对象的双眼瞳孔中心水平距离，重复3次计算平均值（保留小数点后一位）（图6）。

1.3 统计学分析

       连续变量以均值±标准差（正态分布）或中位数（四分位距）（非正态分布）表示，分类变量以频数（百分比）描述。

      本研究采用Bland-Altman分析评估Eye-ruler2与五合一测量尺在配镜参数测量中的一致性，计算平均偏差（Bias）及其95%一致性界限（limits of agreement, LoA）。计算两种测量方法对同一配镜参数的组内相关系数（ICC），依据标准^[16]分级：ICC<0.50为"差"，0.50~0.74为"中等"，0.75~0.90为"较好"，ICC>0.90为"极好"。

       为评估基于镜眼距、前倾角和面弯配镜参数对总屈光变化量（总屈光变化量=镜眼距屈光变化量+前倾角屈光变化量+面弯屈光变化量）的贡献程度，首先计算各参数的屈光变化量（其中镜眼距屈光变化量采用顶点力补偿公式^[3]计算，前倾角和面弯屈光变化量采用马丁公式^[3]计算，变化量均保留原始正负符号），随后取其绝对值并求和得到总绝对变化量（|Δ镜眼距| + |Δ前倾角| + |Δ面弯|）。各参数的贡献程度以绝对变化量占比表示（即单个参数绝对变化量与总绝对变化量的百分比）。各个屈光变化量同时存在正负值，旨在通过绝对值转换消除了参数间正负抵消效应。采用Friedman检验和符号秩和检验比较3个参数的绝对贡献度百分比差异。采用Spearman秩相关分析评估总屈光变化量与等效球镜度的相关性。以局部加权散点平滑（Lowess）曲线展示总屈光变化量、镜眼距屈光变化量、前倾角屈光变化量及面弯屈光变化量与等效球镜度（SER）的关系。

       采用Stata 16.0（StataCorp LP, USA）进行统计分析，α=0.05。

2 结果

2.1 研究对象基本情况

       本研究共纳入103名大学生，其中等效球镜度（左眼/右眼）、右眼镜眼距（Eye-ruler2/五合一测量尺）、左眼镜眼距（Eye-ruler2/五合一测量尺）、前倾角（Eye-ruler2/五合一测量尺）、面弯（Eye-ruler2/五合一测量尺）等数据见表1。

2.2 Eye-ruler2与五合一测量尺测量参数结果的一致性分析

       在Bland-Altman图中展示了Eye-ruler2和五合一测量尺在左右眼镜眼距、前倾角、面弯和瞳距测量中的一致性（图7）。

     右眼镜眼距、左眼镜眼距、前倾角、面弯和瞳距测量平均偏差和95%LoA数据见表2；; 右眼镜眼距、左眼镜眼距、前倾角、面弯和瞳距测量分别有4.85%（5/103）、5.83%（6/103）、5.83%（6/103）、5.83%（6/103）和3.88%（4/103）测量值超出95%LoA。右眼镜眼距和瞳距测量时线点占比小于5%，表明Eye-ruler2和五合一测量尺在这两个测量参数中具有一定程度的一致性。

       一致性分析显示，瞳距测量具有极好的一致性（ICC=0.95），镜眼距测量右眼（ICC=0.76）和左眼（ICC=0.80）分别达到较好一致性水平，前倾角一致性中等（ICC=0.67），而面弯测量一致性较差（ICC=0.37）。

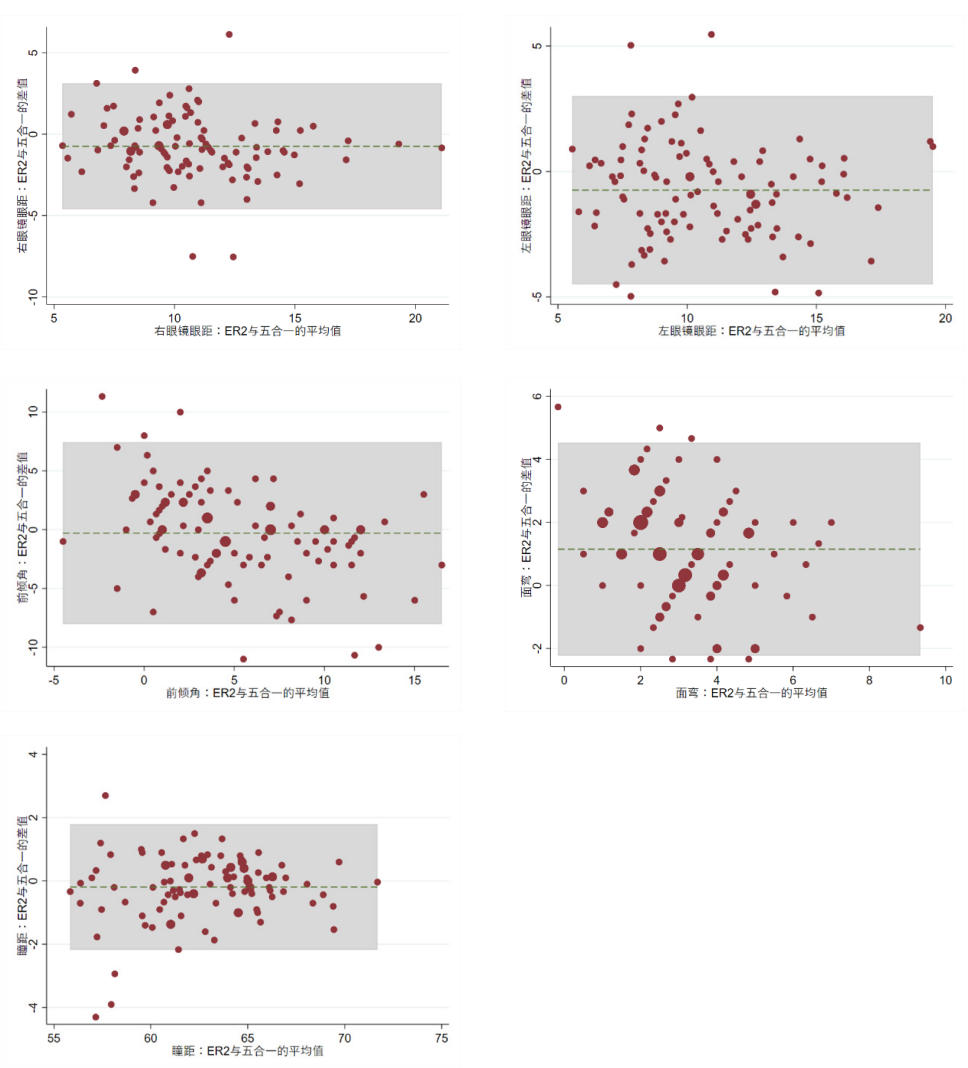
最左列从上到下分别代表Eye-ruler2和五合一测量尺测量右眼镜眼距、前倾角和瞳距参数的Bland-Altman图，最右列从上到下分别代表Eye-ruler2和五合一测量尺测量左眼镜眼距、面弯参数的Bland-Altman图；图中绿色虚线为Eye-ruler2与五合一测量尺分别测量相同配镜参数的差值均值；图中阴影的上下线为一致性界限LoA的上下限。

Left column (top to bottom): Bland-Altman plots for right-eye monocular vertex distance, pantoscopic tilt, and monocular PD measured by Eye-ruler2 and Combination Gauge respectively; Right column (top to bottom):Bland-Altman plots for left-eye monocular vertex distance and face form measured by Eye-ruler2 and Combination Gauge respectively; Green dashed line: Mean difference between device measurements for identical spectacle parameters; Shaded area boundaries: Upper and lower limits of agreement (LoA, 95% CI).

ICC: 组内相关系数；Bias:平均偏差；CI：置信区间；LoA：一致性界限;五合一：五合一测量尺；ER2：Eye-ruler2。

ICC: intraclass correlation coefficient; Bias: mean difference between methods; CI: 95% 

2.3 各项配镜参数对屈光度的绝对贡献

       本研究分析了两种测量技术下配镜参数对屈光度的绝对贡献，Eye-ruler2与传统五合一分析结果相似（表3、4）。

       Eye-ruler2所测量的右眼镜眼距、前倾角和面弯对于处方的总屈光变化量均值为-0.12 D；右眼镜眼距屈光变化量均值为-0.04 D；前倾角屈光变化量均值为-0.06 D；面弯屈光变化量均值为-0.01 D；其中各项参数屈光变化量绝对值占比的均值分别为右眼镜眼距40.61%、前倾角41.83%、面弯16.57%（表3）。符号秩检验显示，前倾角与镜眼距对屈光度的绝对贡献（屈光变化量绝对值的占比）比较差异无统计学意义（P=0.851），而面弯与镜眼距及前倾角对屈光度的绝对贡献比较差异均有统计学意义（P值均 <0.001）。

OD：右眼。

OD: Right eye.

OD：右眼。

OD: right eye.

2.4 原等效球镜度与各配镜参数影响下屈光变化量之间的关系

       局部加权回归曲线图中显示总屈光变化量与原等效球镜度呈正相关（r_s为 0.647~0.722之间，P均小于 <0.001），随着眼镜等效球镜度近视度数的增加，总屈光变化量也在逐渐增加（图8）。当眼镜等效球镜度在-6.00 D内时，总屈光变化量主要受前倾角影响；在-6.00 D范围外时，曲线局部提示镜眼距对屈光变化量的影响更大（图8）。

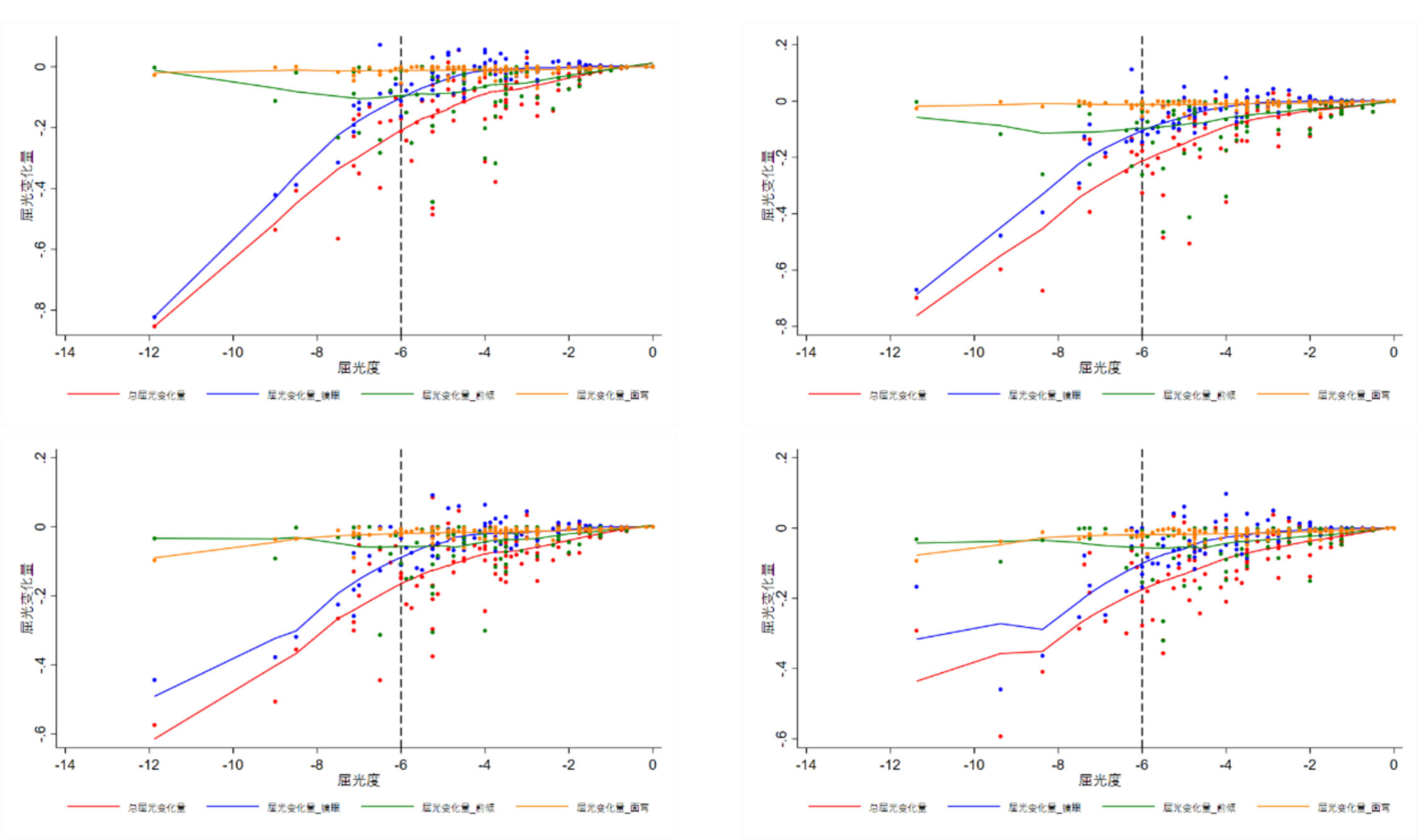
最左列从上到下分别代表Eye-ruler2和五合一测量尺测量下右眼各屈光变化量局部加权回归曲线图，最右列从上到下分别代表Eye-ruler2和五合一测量尺测量下左眼各屈光变化量局部加权回归曲线图；总屈光变化量：测量各参数影响下总体屈光变化量；屈光变化量_镜眼：镜眼距影响下的屈光变化量；屈光变化量_前倾：前倾角影响下的屈光变化量；屈光变化量_面弯：面弯影响下的屈光变化量。

Left column (top to bottom): Lowess regression curves for refractive changes in the right eye measured by Eye-ruler2 and Combination Gauge, respectively. Right column (top to bottom): Lowess regression curves for refractive changes in the left eye measured by Eye-ruler2 and Combination Gauge, respectively; Total refractive change: Overall refractive change induced by all parameters; Refractive change_VD: Change induced by vertex distance; Refractive change_PT: Change induced by pantoscopic tilt; Refractive change_FF: Change induced by face form.

3 讨论

       本研究对数字化新技术Eye-ruler2与传统方法五合一测量尺在配镜参数（如镜眼距、前倾角、面弯及瞳距）的一致性进行比较。结果显示新技术和传统方法在瞳距、镜眼距、前倾角的一致性好，而面弯一致性较差。Eye-ruler2具有自动识别图像与头位校准功能，通过 iPad上专用的镜头为受检者近距离（60～75 cm)拍摄正面及侧面照片（图1、2), 并通过数字化照片分析，即可获得一系列参数结果，具有简便快捷、易操作和受检者体验感好等优点。而传统测量方法，不仅依赖操作者的熟练程度，而且对每项参数测量都需经过专门培训方可掌握，如测量镜眼距需准确定位角膜顶点及镜片后表面位置等，这就需要测量者了解眼睛的解剖等专业知识。笔者认为数字化新技术可以取代传统方法获得各项配镜参数，Eye-ruler2在推广使用上较五合一测量尺具有更大优势。

       本研究结果显示两种技术测量镜眼距的一致性良好（右眼镜眼距ICC=0.76，左眼镜眼距ICC=0.80）。镜眼距是角膜顶点与镜片后表面之间的距离，笔者团队用传统方法五合一测量尺测量时发现，镜片后表面顶点较难判断，因为镜片是透明的，而Eye-ruler2通过自动图像识别技术可获得相关数据，解决临床经验不足可能导致的误差。前倾角是镜片与面部冠状面夹角，两种技术测量呈现中等一致性（ICC=0.67），主要原因是传统方法测量前倾角时容易受到受检者头位影响，比如下巴上扬或者低头的习惯，都会影响传统方法测量的前倾角度数；而Eye-ruler2在拍照中会提示受检者头位调整到正确位置，从而减少了因为头位偏差导致的前倾角误差，所以我们认为Eye-ruler2的测量结果会更接近眼镜实际的前倾角度数。面弯为镜框水平面的弯曲弧度，面弯结果显示一致性差（ICC=0.37），传统工具在离体状态下测得的值较Eye-ruler2真实戴镜状态的值高1.15度。笔者认为一致性差有以下原因：一是两种技术在面弯测量上存在显著的方法学差异，传统的面弯测量是在离体状态下（即手持眼镜架在桌面对照卡尺测得），而Eye-ruler2则是在真实戴镜状态下测得；二是在戴镜状态下和离体状态下面弯可能本身就不同，因为镜框材质（金属/板材）和鼻托压力可能动态影响面弯角度，所以Eye-ruler2面弯结果应该更接近实际佩戴的状态。

       本研究还通过分析各参数对处方度数的影响，为评估实际戴镜度数效果提供量化依据，即探讨临床在试镜架验配的配镜处方和实际佩戴的框架眼镜度数的效果差距的问题。既往研究可能更关注镜眼距对处方的理论影响，如-7.00 D近视眼镜处方（默认镜眼距12 mm），而当实际框架眼镜的镜眼距为17 mm时，若单纯考虑镜眼距的影响，则实际戴镜效果为-6.75 D^[2]。前倾角和面弯目前仅在少量个性化验配渐进镜时作为常规测量参数。根据马丁公式，对于近视眼来说，前倾角会导致额外的水平顺规散光^{[3, 8]}，面弯会导致垂直逆规散光^[3]，远视眼则相反，而散光作为初阶像差对于视觉质量的影响至关重要^[17]。本研究显示，镜眼距与前倾角对配镜处方等效屈光度的绝对贡献等同（P=0.851），分别为40.6%与41.8%。同时结果显示当处方等效球镜度在-6.00 D内（中低度近视）时，前倾角对处方度数的影响更大，这提示我们在常规验配时需更加关注前倾角因素；而在-6.00 D（高度近视）以上时，镜眼距的影响更大（图8），这提示我们在面对高度近视人群（<-6.00 D）精准验配时更需要关注到镜眼距因素，这与既往的理论研究结果^[2-3]相似。在真实世界，眼镜不能达到处方的实际效果的问题普遍存在。因为本研究对象主要为中度近视的大学生，总处方度数影响均值为-0.12 D。姚婷婷等^[18]关于精准验光的研究中，发现0.05 D进阶处方相比0.25 D进阶处方，矫正视力和空间频率对比敏感度更好，这说明随着0.05 D精准验光等研究的不断深入，对于更精准配镜的需求也将不断提升。且随着视觉质量需求向立体视锐度、像差容忍度等高阶指标延伸时，未来个性化定制的眼镜将为满足更清晰和舒适的视觉质量要求提供有效途径^[19]，本文的结果将为临床配镜高质量的发展提供依据。

       本研究显示，Eye-ruler2测得前倾角均值为5.36°，低于临床范围（8°~15°）^[20]和黄种人推荐范围（8°~10°）^[3]，这提示真实佩戴框架眼镜的前倾角度数和既往理论存在不一致情况。提示我们是否亚洲人群因鼻梁较高加索人种更低平的原因造成，是否需重新审视及修正临床参考范围（如将8°~10°下调至5°~8°）还需更多研究数据来证实。面弯虽在总体处方度数中影响有限（占比16.57%），但对于有些特殊设计的太阳镜或者运动眼镜的近视眼镜个性化定制，建议全面考虑眼镜架各参数对度数的影响，计算实际眼镜处方，提升用户舒适度。

       本研究仍存在以下局限性：1）样本量较少可能影响数据结果，日后研究需扩大样本量。2）本文未能涵盖参数对于视觉质量的影响，下一步可结合波前像差仪等设备，量化参数偏差与主观视觉质量的关联性。3）研究对象未进行分类，将来建议有条件下可以对高度近视与中低度近视研究对象进行分组研究。4）Keating等^[21]的研究讨论了前倾角和面弯的组合公式，Harris等^[22]利用旋转矩阵来表示空间中的旋转，并借鉴了三阶光学中关于斜中心折射研究前倾角的影响；本研究仅采用马丁公式进行计算前倾角和面弯对于处方的影响，未来可结合其他研究进一步探究其影响。5）本研究未进行瞳高、单眼瞳距等参数一致性的比对，因为本文聚焦于处方度数的影响，并未探究棱镜效果所带来的视疲劳等影响，未来可结合双眼视功能检查进行深入研究。在目前个性化配镜^[23-25]及镜架定制^[26-28]逐渐普及的前景下，镜眼距、前倾角和面弯的个性化参数定制逐渐呈现大众化的趋势。我们建议视光师对于镜眼距、前倾角和面弯这三个参数更加关注，共同为民众视觉质量提升助力，最终实现从光学矫正到视觉质量提升的跨越。

       综上所述，Eye-ruler2与五合一测量尺在该研究中测量参数的一致性好，数字化新技术可以替代传统测量方法并推广使用。镜眼距和前倾角对于处方度数的影响等同，当处方度数在-6.00 D以内时前倾角影响更大，在-6.00 D以上时则镜眼距的影响更大；面弯虽然对处方度数影响较其他参数更小，但其造成逆规散光对视觉质量影响可能较大。所以我们认为在未来个性化配镜的前景下，在配镜时常态化测量镜眼距、前倾角和面弯，可以为个性化镜片定制提供更多依据，以提升群众视觉质量。

声明

在论文撰写中无使用生成式人工智能。论文撰写中的所有内容均由作者独立完成，并对出版物的真实性和准确性承担全部责任。

利益冲突  

所有作者均声明不存在利益冲突。

开放获取声明

本文适用于知识共享许可协议(Creative Commons)，允许第三方用户按照署名(BY)-非商业性使用(NC)-禁止演绎(ND)(CC BY-NC-ND)的方式共享，即允许第三方对本刊发表的文章进行复制、发行、展览、表演、放映、广播或通过信息网络向公众传播，但在这些过程中必须保留作者署名、仅限于非商业性目的、不得进行演绎创作。